哈夫曼树
哈夫曼树也叫最优二叉树(哈夫曼树)
定义
名词解释
| 名词 | 解释 |
|---|---|
| 路径长度 | 根结点到第L层结点路径长度为L-1 |
| 树的带权路径长度(WPL) | 树中所有叶子结点的带权路径长度之和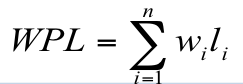 其中,n表示叶子结点的数目,wi和li分别表示叶子结点ki的权值和树根结点到叶子结点ki之间的路径长度。 |
 |
|
特点
- 哈夫曼树中权越大的叶子离根越近(WPL最小的二叉树)
- 具有相同带权结点的哈夫曼树不惟一
- 哈夫曼树的结点的度数为 0 或 2, 没有度为 1 的结点;
- 包含 n 个叶子结点的哈夫曼树中共有 2n – 1 个结点。
- 包含 n 棵树的森林要经过 n–1 次合并才能形成哈夫曼树,共产生 n–1 个新结点

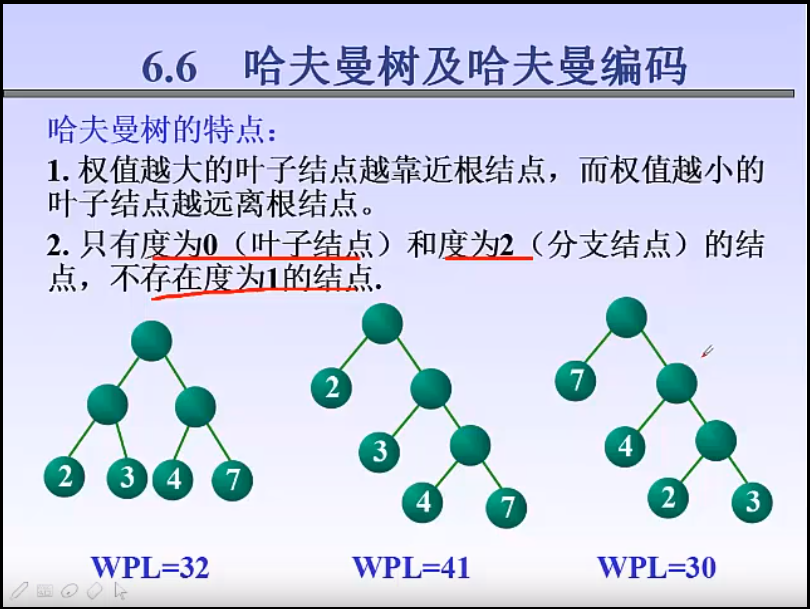
WPL 最小的值所属的树即为哈夫曼树
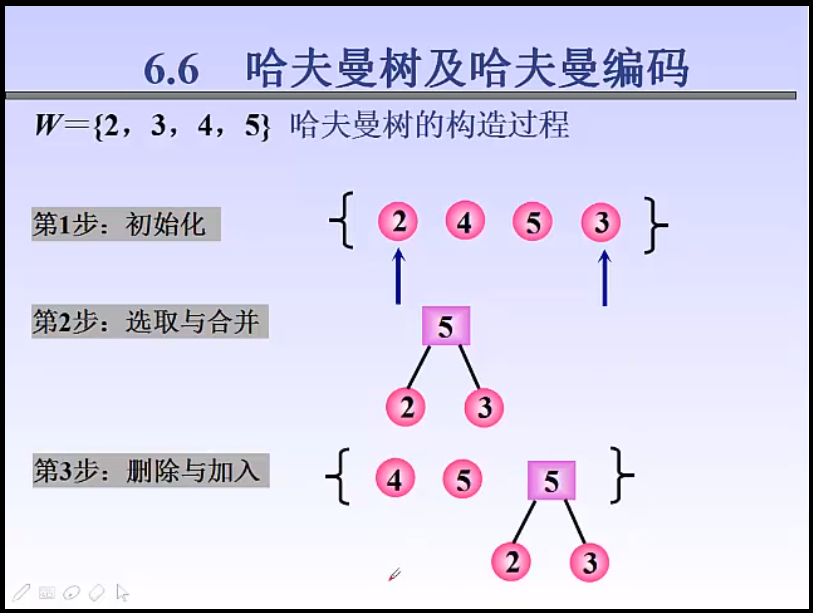
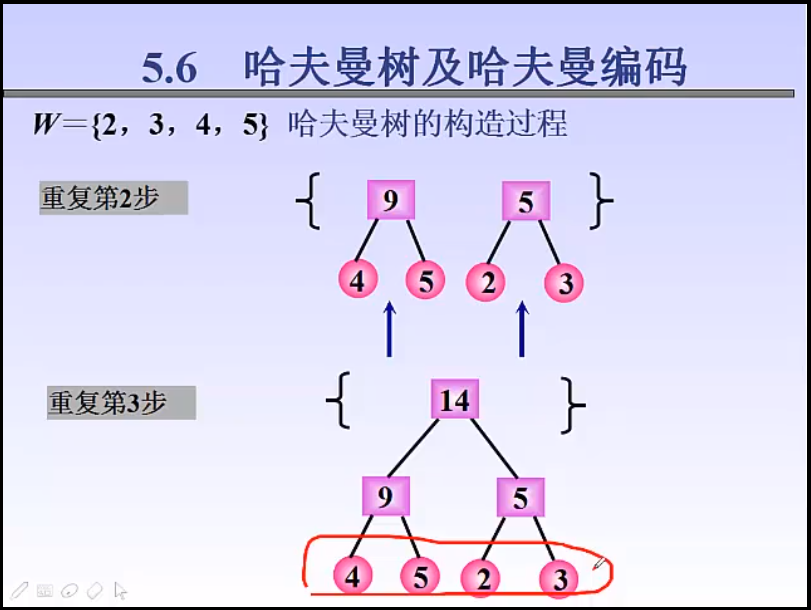

哈夫曼创建

为什么数组buffTree[2n-1] 的大小是2n-1,是因为n个子节点构成的树节点最多的个数是2n-1个
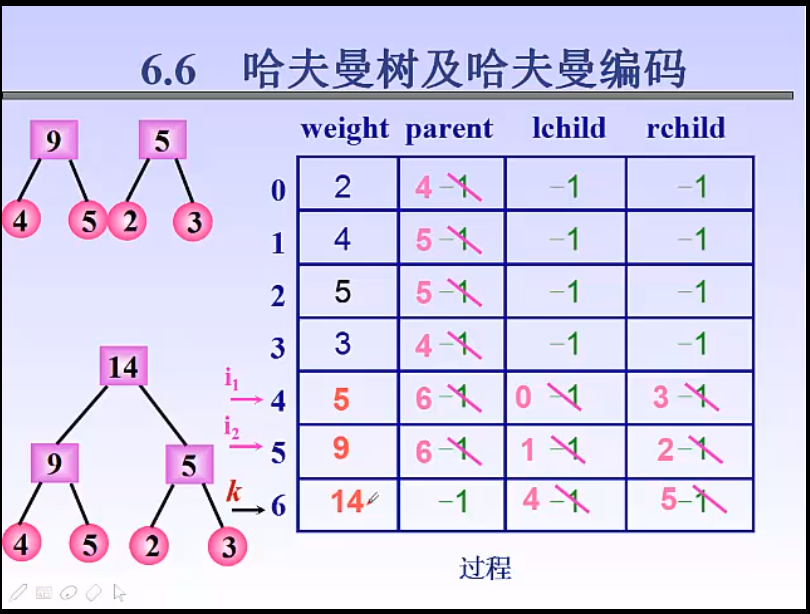

哈夫曼树编码
前缀编码

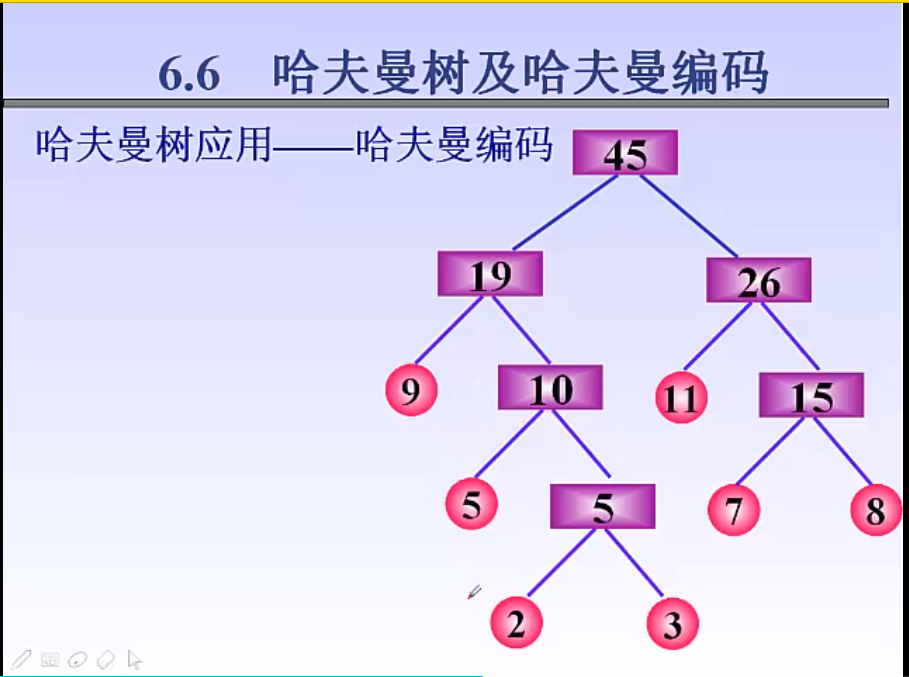
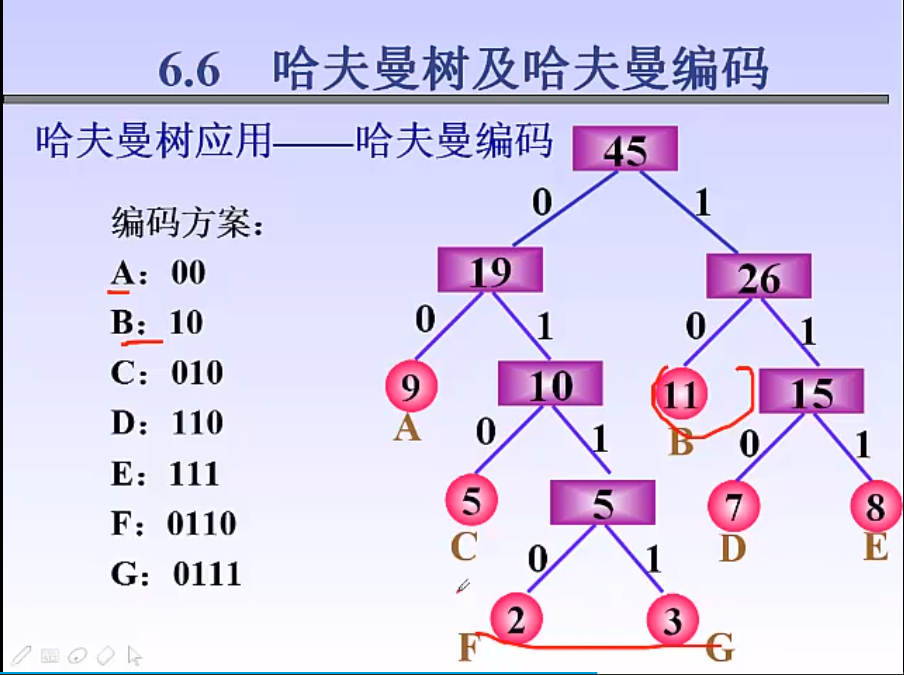
特点:
权值越高的叶子节点越靠近根节点




